Mathematical averages, also known as mathematical means, are statistical measures that are computed based on mathematical operations. The main types of mathematical averages include:
1. Arithmetic Mean (AM)
- The sum of all values divided by the total number of values.
- Formula:
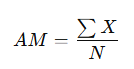
- Example: The average of 10, 20, and 30 is (10+20+30) / 3 = 20.
2. Geometric Mean (GM)
- The nth root of the product of all values.
- Formula:
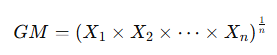
- Used when values have exponential or multiplicative relationships (e.g., growth rates).
- Example: The GM of 2, 4, and 8 is (2 × 4 × 8)^(1/3) = 4.
3. Harmonic Mean (HM)
- The reciprocal of the arithmetic mean of reciprocals.
- Formula:
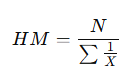
- Used when dealing with rates (e.g., speed, finance).
- Example: The HM of 2, 4, and 8 is 3 / (1/2 + 1/4 + 1/8) = 3.43.
4. Quadratic Mean (Root Mean Square – RMS)
- The square root of the average of the squares of values.
- Formula:
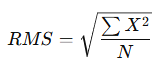
- Used in physics and engineering.
Key Differences:
| Type of Mean | When to Use |
|---|---|
| Arithmetic Mean | General average calculation |
| Geometric Mean | Growth rates (finance, population, etc.) |
| Harmonic Mean | Rates and ratios (speed, financial returns) |
| Quadratic Mean | Variability in physical sciences and engineering |
Food for thought : Is Mode a Mathematical Average?
-
Mathematical averages (like mean, geometric mean, and harmonic mean) involve arithmetic calculations like summation, division, or exponentiation.
-
Mode is simply the most frequently occurring value, without any mathematical computation.