The Poisson distribution is a probability distribution that models the number of events that occur within a fixed interval of time or space, given that these events happen with a known constant mean rate and independently of each other. It’s often used in situations where you’re counting the number of occurrences of some event, like:

• The number of phone calls at a call center in an hour

• The number of accidents at a traffic intersection during a day

• The number of emails received per hour

Key Features of the Poisson Distribution:

1. Discreteness: It’s a discrete probability distribution, which means it models counts of events (like 0, 1, 2, 3… events).

2. Constant Rate (λ): The events occur at an average rate of λ (lambda), which is the expected number of events per interval.

3. Independence: The occurrence of an event in one interval does not affect the occurrence of an event in another interval.

4. Rare Events: The events modeled by the Poisson distribution tend to be rare or uncommon, though they can happen at any point in time.

Poisson Distribution Formula:

The probability of observing exactly k events in an interval is given by the formula:

Example:

Suppose a bookstore receives, on average, 3 customers per hour. You want to know the probability of receiving exactly 5 customers in an hour.

Here, λ = 3 (the average number of customers per hour), and we are interested in k = 5 (exactly 5 customers). Using the formula:

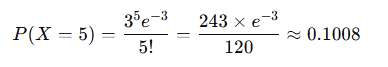
So, the probability of exactly 5 customers coming in the next hour is about 0.1008 (or 10.08%).

When to Use the Poisson Distribution:

• When the events are independent.

• When events happen at a constant average rate.

• When you are counting occurrences over a fixed time period or in a fixed area/volume.

The Poisson distribution is a useful model for many real-world phenomena, particularly in situations involving rare events over time or space.