Imagine you have the first $n$ natural numbers, like 1, 2, 3, 4, and so on. These are the numbers you want to find the “standard deviation” for.

What is Standard Deviation?

First, let me tell you what standard deviation is. It’s just a way to measure how spread out the numbers are. If the numbers are very close to each other, the standard deviation is small. If the numbers are far apart, the standard deviation is big.

Step 1: Find the Average

To start, we need to find the “average” of the numbers. The average is just the middle value of the numbers.

For the first n numbers, we can find the average by adding up all the numbers and dividing by how many numbers there are.

For example, for the first 5 numbers: 1, 2, 3, 4, and 5:
Average = [1+2+3+4+5] / 5 = 15 / 5 = 3

So, the average is 3.

Step 2: Find How Far Each Number Is from the Average

Next, we look at how far each number is from the average. This is called the “difference.”

For example, for the first 5 numbers:

• How far is 1 from 3? It’s 2 steps away.
• How far is 2 from 3? It’s 1 step away.
• How far is 3 from 3? It’s 0 steps away.
• How far is 4 from 3? It’s 1 step away.
• How far is 5 from 3? It’s 2 steps away.

Step 3: Find the “Squared” Differences

Now, to make sure we don’t get negative numbers when we look at differences, we “square” each difference. Squaring means multiplying the number by itself.

For example:

• The difference for 1 was 2, so 2×2=4.
• The difference for 2 was 1, so 1×1=1.
• The difference for 3 was 0, so 0×0=0.
• The difference for 4 was 1, so 1×1=1.
• The difference for 5 was 2, so 2×2=4.

Step 4: Find the Average of the Squared Differences

Now we find the average of all these squared differences. This helps us see, on average, how far the numbers are from the average.

For example, the squared differences are 4, 1, 0, 1, and 4. We add them up:

4 + 1 + 0 + 1 + 4 = 10

Then, we divide by how many numbers there are (5 numbers):

Average of squared differences = 10 / 5 ​= 2

Step 5: Take the Square Root

Finally, to get the standard deviation, we take the square root of this average. The square root is just the opposite of squaring a number. So, for our example:

2^0.5 ​≈1.41

This is the standard deviation for the first 5 numbers.

General Formula

When you do this for any number of numbers, you can use a formula. The standard deviation of the first $n$ numbers is:

​​

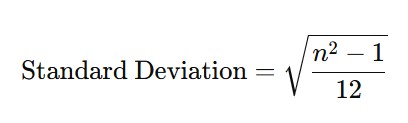
So, that’s how you find the “spread” or “spread-out-ness” of the first $n$ natural numbers!